Optimization of ship sterns with CFD

Design of hull lines for energy efficient ships continues to be one of the major challenges for the ship designers. Based on knowledge in hydrodynamics, experience from towing tank tests and some intuition the designers can improve the lines. This is slow and costly process that requires validation data from experiments and sea trials. The introduction of CFD methods made it possible to evaluate more hull variants between tests and new generations of ships could be developed faster and with larger improvements. This design process can be seen as a manual optimization, where the designer creates the new variants guided by the results from CFD computations and tests. In an automatic optimization the optimum hull is found given the prescribed objectives, constraints and design space. One could imagine that this makes the ship designer redundant, but this is not the case. It is a new tool that can help the designer to develop even better hull forms. Knowledge and experience are required to define the geometry variations and constraints, and to find the best compromise between hulls optimized for different speeds, drafts and other conditions. The automatic optimization is an extension of the traditional way of using CFD.

Automatic optimization was first applied successfully on fore-body optimizations to minimize the wave resistance. Optimization of the ship stern requires more computational resources. Another complication is that there are two major effects, the resistance and the propeller efficiency, that determines the ship performance. The first stern optimizations considered only the resistance in towed condition, while the propeller efficiency was estimated from wake quality measures. This approach was in general not successful. In this article we show another approach for optimizing the ship performance by directly minimizing the delivered power [3], [4], [5].

The computational times for resistance and self-propulsion were significantly reduced in SHIPFLOW version 6. In fact, the improvements were so large that it became possible to carry out optimizations with a small cluster or even a workstation within reasonable time as will be shown in this article.

Case description

The Japanese Bulk Carrier (JBC) test case [1] from Tokyo Workshop 2015 was chosen as the base hull for the optimizations. The test case was developed for validating resistance and self-propulsion computations on a ship with and without an energy saving device. The ship particulars and service conditions are found in the table below.

Optimizations

The purpose of this study is to demonstrate optimizations of the aft-body for resistance and delivered power, and to draw conclusions from the two approaches. CAESES from FRIENSHIP-SYSTEMS was used for the geometry variations and optimization and SHIPFLOW RANS 6.0 [2] for resistance and self-propulsion computations. A partially parametric technique was chosen for the hull shape modifications. It was set up in such way that four of the most important hull features

• bilge radius
• keel line profile of bossing
• skeg (gondola) width
• section fullness above skeg

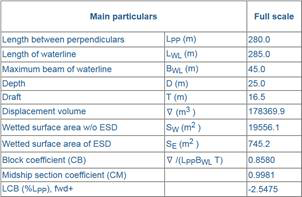
could be controlled with a few parameters. Each of the four features were controlled by delta shift surfaces. Figure 1 shows the delta shift for changing the bilge radius and an example of the resulting changes of the frames.

The NSGA-II genetic algorithm was chosen for the optimization. The method has a good ability to explore a large design space without getting trapped in a local minimum.

Resistance optimization

The first optimization is set up to minimize the resistance (towed condition). A grid consisting of 1.2 million cells was used for the RANS computations [7], corresponding to SHIPFLOW’s FINE grid option. The original hull surface was imported from an IGES-file and after the shape variation the new surface was exported to SHIPFLOW that computes the new grid automatically. The computation took about 15 minutes per case on a workstation (1x Intel i7 5960X, 8 Cores, and 3.0 GHz). About 120 designs in total were investigated (5 generations with a population of 24 in each generation). The history from the optimization is shown in Figure 2.

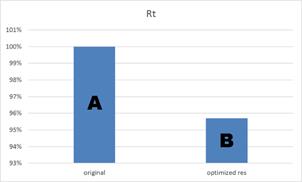
The resistance for the optimized hull was reduced by 4%. This is shown in Figure 3. Hull A being the original hull and hull B the hull optimized for resistance. No constraints were considered and the displacement was reduced by 0.4%.

Self-propulsion optimization

The second optimization minimizes the delivered power (Pd) in self-propelled condition at model scale. The inbuilt lifting line propeller model [6] in SHIPFLOW was used in the computations. The grid consists of about 3.0 million cells in total. The increased number is mainly due to the loss of symmetry and from an additional overlapping grid component required for the lifting line model. The grids were computed automatically from IGES using the SHIPFLOW MEDIUM grid option with a refinement around the stern. The optimization was run for 4 generation consisting of a population of 24 each. Four cases were computed in parallel on a small cluster consisting with 4 nodes equipped with 2x Intel Xeon X5675, 2x6 Cores each. The CAESES Resource Manager was used to distribute the jobs. The optimization took about 24 hours to complete.

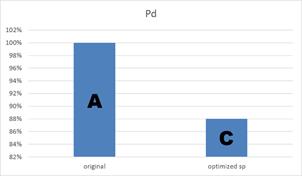
The delivered power was reduced by 10% for the optimized hull, see Figure 4. Hull A being the original hull and hull C the hull optimized for delivered power. No constraints were applied in this case and the displacement was reduced by 0.4% making it equal to the displacement of the hull B.

Comparisons

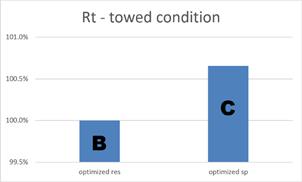
Hull C, optimized for Pd, was re-computed for the towed condition and the resistance was compared to hull B, optimized for resistance, Figure 5. The latter has a lower resistance as expected. Similarly hull B was also re-computed in self-propelled condition and Pd was compared to hull C, Figure 6. The comparison clearly shows that the increased propeller efficiency of hull C outbalances the higher resistance it has compared to hull B.

Conclusions

The two optimizations clearly demonstrates the importance to optimize the ship stern in propelled condition and minimize the delivered power. Hull modifications can create contradictory results of the two components resistance and propeller efficiency. In our example the gain in the propeller efficiency was large enough to compensate for the increase in resistance.

Conclusions and recommendations:

• SHIPFLOW is an efficient tool for self propulsion optimizations
• Partially parametric modelling delivered by CAESES gives very good control and flexibility of hull modifications, both global and local
• SHIPFLOW and CAESES is an excellent environment for hydrodynamic optimizations
• Optimization of hulls in self-propulsion condition gives the best results

Constraints for hard points and displacement as well as assessments of cavitation would normally be required in a commercial application. However, this will not affect the conclusion made in this article.

Optimization directly at full scale will circumvent the need for extrapolation from model scale. This will be demonstrated in the next article.

References

1. (2015). Tokyo 2015 A Workshop on CFD in Ship Hydrodynamics. Retrieved from http://www.t2015.nmri.go.jp/
2. Broberg, L., Regnström, B., Östberg, M., (2007) ‘SHIPFLOW User Manual and Theoretical Manual’, FLOWTECH International AB, Gothenburg, Sweden
3. Broberg, L., & Orych, M. (2012). An Efficient Numerical Technique to Simulate the Propeller Hull Interaction. International Journal of Innovative Research & Development, 14. PDF
4. Han, K J (2008) “Numerical optimization of hull/propeller/rudder configurations”, PhD thesis, Department of Naval Architecture and Ocean Engineering, Division of Hydrodynamics, Chalmers University of Technology, Gothenburg, Sweden.
5. Kim Keunjae and Li Daqing (2010): “Estimation of Numerical Uncertainty of SHIPFLOW in Self-propulsion Simulation of KCS”, G2010, Gothenburg 2010 Workshop on CFD in Ship Hydrodynamics
6. Zhang D H (1990) Numerical computation of ship stern/propeller flow. Ph D thesis. Department of Naval Architecture and Ocean Engineering. Chalmers University of Technology
7. Regnström, B., Broberg, L., & Larsson L. (2000) “Ship stern flow calculations on overlapping composite grids”, 23^rd Symposium on Naval Hydrodynamics, Val de Reuil, France. PDF
8. Larsson, L., Han, K. J., Bark, G., Regnstrom, B., and Bathfield N., “Numerical optimization of propeller-hull configuration at full scale”, World Maritime Technology Conference, March, 2006, London. PDF